Ma3 Ch1: Etymologie "fonction"
Comparons des sources
-----
"Fonction : du latin functio, accomplissement (de fungi, s'acquitter de), exécution. Utilisé en 1637 par le mathématicien et philosophe français René Descartes, pour désigner une puissance xn d'une x.
Le fonction
apparait dans un manuscrit en latin, "Methodus tangentium inversa, seu
de fuctionibus", du mathématicien et philosophe allemand Wilhelm
Gottfried Leibniz (1646-1716) en 1673 . Il l'appliquait à différentes
caractéristiques d'une courbe, comme par exemple sa pente. La
la plus utilisée actuellement a été énoncée en 1829."
Source : http://trucsmaths.free.fr (le 12.8.08)
----
"Si le mot est emprunté sous la forme simplifié funcion (1370) au latin functio
"accomplissement, exécution" en français courant [7], Descartes
(1597-1650) l'utilise en mathématique pour désigner une
algébrique correspondant à un graphique. Au 18ème Euler (1707-1783)
propose l'idée qu'une suite de courbes, donc d'expressions,
représentait une fonction.
Ailleurs,
on dit que c'est Leibniz (1646-1716) qui utilise le mot pour la
première fois en mathématiques en 1673, que la première fut
donnée par J.Bernouilli (1654-1705) et que le symbole f(.) a été
introduit par Euler en 1734.
Alors, restons prudent..."
Source : http://www.math93.com/ (le 12.8.08)
----
"La notion de fonction en tant que correspondance entre deux types
d'objet est relativement ancienne. Mais le n'apparait qu'à la fin
du XVIIe siècle sous la plume de Leibniz en 1694 , il s'agit alors de fonction associée à une courbe géométrique : Leibniz dit ainsi que l'abscisse, l'ordonnée ou le rayon de courbure d'une courbe en un point M est une fonction du point M. Dans la même époque, Newton parle de fluente
pour des quantités dépendant d'une qu'il appelle le temps
(tout en précisant que le rôle joué par le temps, peut l'être par une
autre quantité). La notation sous la forme f ne s'est pas mise en place tout de suite. Jean Bernoulli propose d'appeler X la fonction de x, Leibniz invente une notation permettant de travailler sur plusieurs fonctions différentes :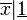 
et 
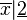sont ainsi deux fonctions dépendant de x. La notation fx apparait chez Euler
en 1734. Les fonctions sont alors toujours à valeurs numériques
(réelles ou complexes) et possèdent en outre des propriétés
restrictives (liées à une algébrique, continuité eulérienne,
développable en série entière...)."
Source : http://fr.wikipedia.org/wiki/Application_(math%C3%A9matiques) (le 12.8.08)